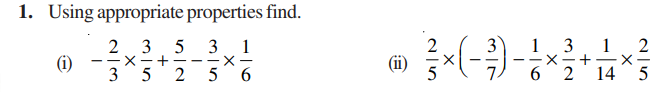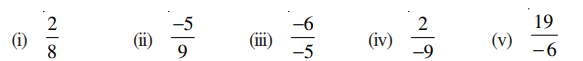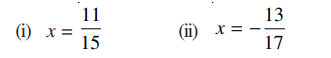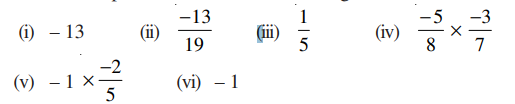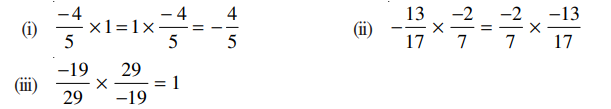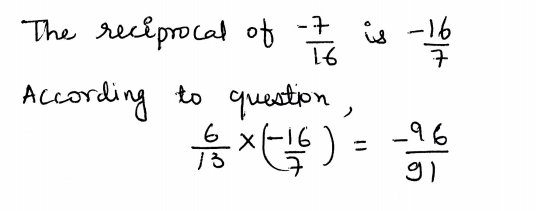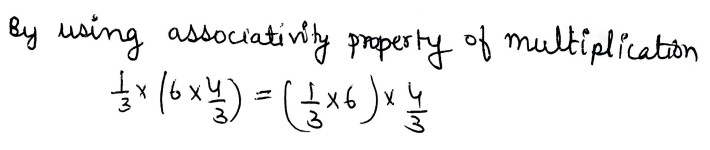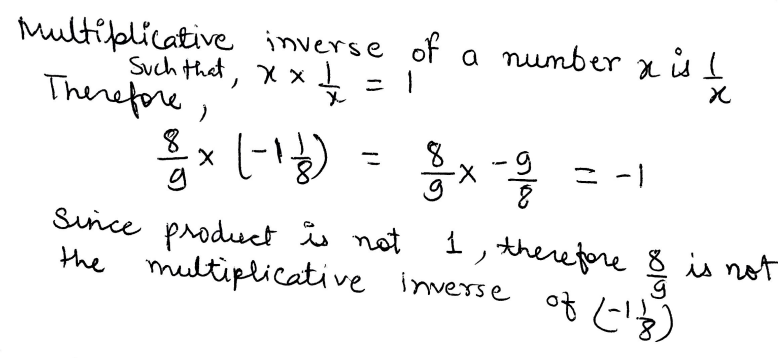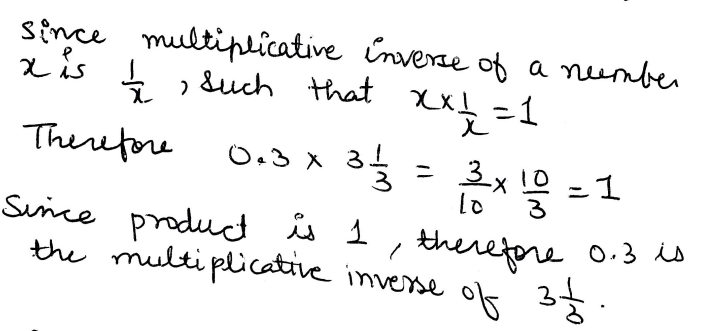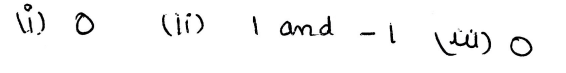NCERT Class 8th Mathematics Solutions – Chapter 1 – Rational Numbers – Exercise 1.1
1. Using appropriate properties find.
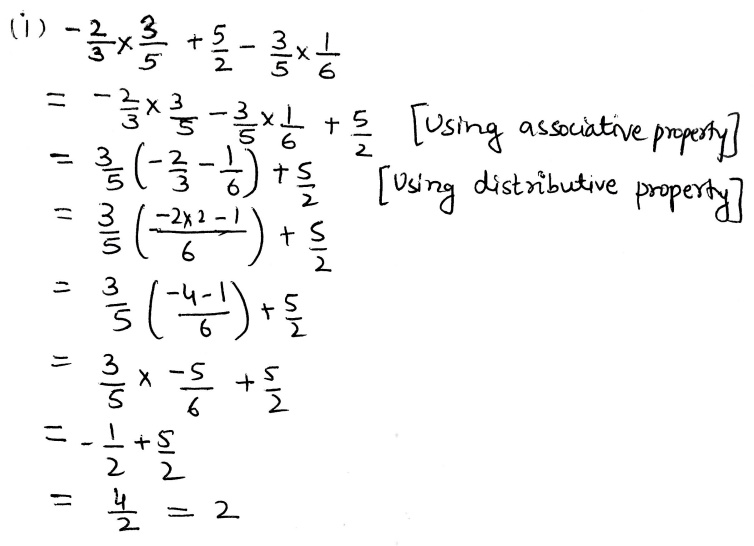

2. Write the additive inverse of each of the following.
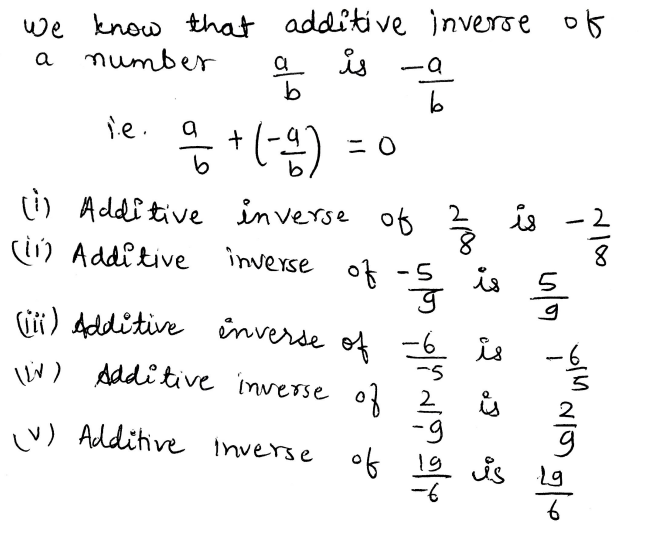
3. Verify that – (– x) = x for.
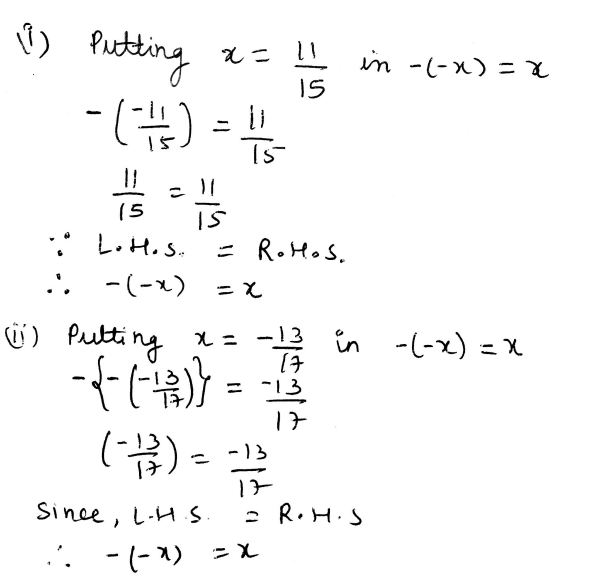
4. Find the multiplicative inverse of the following.

5. Name the property under multiplication used in each of the following.
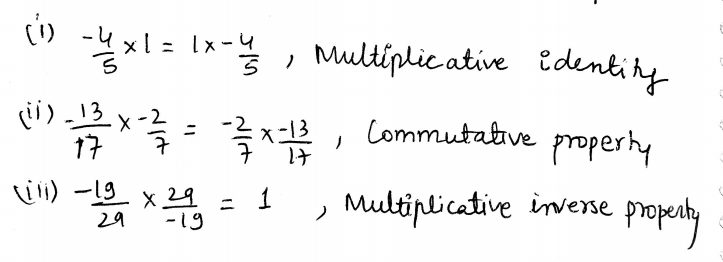
6. Multiply 6/13 by the reciprocal of -7/16
7. Tell what property allows you to compute 1/3 * (6 * 4/3) as (1/3 * 6) * 4/3
8. Is 8/9 the multiplicative inverse of 1 1/8 ? Why or why not?
9. Is 0.3 the multiplicative inverse of 3 1/3 ? Why or why not?
10. Write.
(i) The rational number that does not have a reciprocal.
(ii) The rational numbers that are equal to their reciprocals.
(iii) The rational number that is equal to its negative.
11. Fill in the blanks.
(i) Zero has __No______ reciprocal.
(ii) The numbers __1______ and ____-1____ are their own reciprocals
(iii) The reciprocal of – 5 is ____-1/5____.
(iv) Reciprocal of 1/x , where x ≠ 0 is ____x____.
(v) The product of two rational numbers is always a ___Rational Number____.
(vi) The reciprocal of a positive rational number is ___Positive_____.
You can find the solution for class 7th Mathematics from here
Tags:
Multiplicative inverse, Multiplicative identity, Rational Numbers, Reciprocal, Additive Inverse, Class 8th Mathematics Solutions, Handwritten notes for Class 8th Mathematics, Chapter 1 Class 8th Mathematics Solutions, Detailed solutions for Class 8th Mathematics Solutions, NCERT Class 8th Mathematics Solutions – Chapter 1 – Rational Numbers – Exercise 1.1, NCERT Class 8th Mathematics Solutions – Chapter 1 – Rational Numbers – Exercise 1.1, – Chapter 1 – Rational Numbers – Exercise 1.2 Wikipedia, Solutions for class 8th NCERT Mathematics, Questions and Solutions for Class 8th Mathematics – Exercise 1.1.